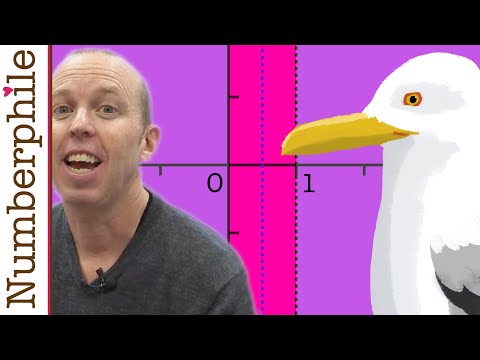
So this is the line where the real part of s is 1.So this is the line where the real part of s is 0.So this is the line where the real part of s is 1.So this is the line where the real part of s is 0.So this is the line where the real part of s is 1.So this is the line where the real part of s is 0.
Brady Yitang Zhang, the famous Chinese mathematician, has done it again. About 10 years ago, he made a big progress in solving the Twin Prime Conjecture, which states that there are an infinite number of prime numbers that differ by 2. Since then, mathematicians have collaborated in the Polymath Project and managed to reduce the gap to 246.
Recently, Yitang Zhang has achieved another possible big result in analytic number theory, related to something called Siegel zeros or Landau-Seigell zeros. This is linked to the Riemann hypothesis, which states that the sum of all positive integers is -1/12. This sum can be extended to all complex numbers using analytic continuation. The interesting thing about this is that it can be linked to prime numbers, and the question is where does this function vanish? We know that the function converges to the right of 1. It is known that the trivial zeros of the zeta function are at -2, -4, and other negative even values. The non-trivial zeros, however, are of more interest and are said to lie in the critical strip between 0 and 1. The Riemann hypothesis states that these non-trivial zeros lie on a line where the real part of the complex number is 1/2. The generalised Riemann hypothesis is a generalisation of this idea, where the sums are weighted with a weighting factor (chi-d of n). These are known as Dirichlet L-functions, and the modulus (D) represents the periodicity of the function. An example of this is the trivial character (D=1) which is always 1, or the principal character (D=2) which is 1 for odd numbers and 0 for even numbers. The Siegel zeros, however, are a counter example to the generalised Riemann hypothesis and are real zeros that lie very close to 1. If a Siegel zero exists, then it should lie on the real line very close to 1. Yitang Zhang was able to prove that there are no zeros in a much thinner region, which had a width of c over log D. He did this by proving a related result which included the number 2022. Even though he has narrowed the search field, to capture the full statement he needs to prove it in a slightly larger region, and as the number is brought down, the region will get bigger until the whole statement is captured. Then all the factors that go into other proofs will kick in, and even this result can have an impact on some mathematical proofs. So that’s that’s the process that’s going on at the moment.
No, I’d like there to be a Siegel zero. New stuff is fun! Most mathematicians would say that there’s probably no Siegel zero, but it’s an illusory proof. There are lots of proofs that rely on the Riemann hypothesis being true, but then it goes deep into proof theory. If we disprove the Reimann hypothesis, it could have implications in physics, as well as in mathematics. The jury is still out amongst the mathematical world and it will take at least a year for the peer review process to be completed. It may be that they spot a small error, or it may be that they agree with the proof. It’s a healthy culture in which, rather than everyone going “oh, it’s wrong”, people will try to work together with the person reviewing the paper and attempt to fix any issues that arise. This has happened in the past when solving Fermat’s Last Theorem. To build a brain that can solve the universe’s wildest problems, check out Brilliant. Their courses, questions, and puzzles have been designed to make learning enjoyable. They even have a bunch of stuff about modular arithmetic, which was touched on by Tony today. You can get 20% off your Brilliant premium subscription by going to brilliant.org/numberphile and you can even give Brilliant as a gift to the future or current genius in your life. Tony’s book, ‘Fantastic Numbers and Where to Find Them’, has been released in the US and the UK covers can be seen in the video description.