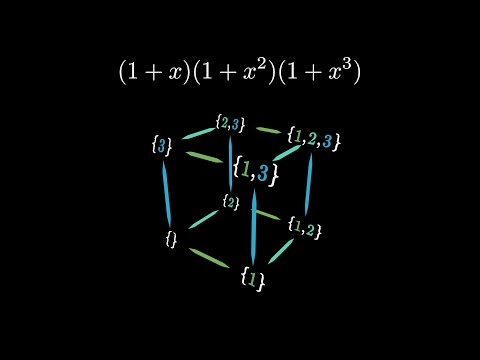In a moment, I will ask you a pretty hard puzzle. Before I do, I want to lead with a spoiler: the way we are going to solve this puzzle involves the use of complex numbers. Even though the puzzle only asks about whole numbers and their sums, complex numbers are still unreasonably useful for discrete math. A famous example of this is how mathematicians understand prime numbers, which involves studying specially designed functions whose inputs and outputs are complex numbers.
Our puzzle for today comes from a book by Titu Andreescu and Zuming Feng, and it asks: “Find the number of subsets of the set one up to two thousand, the sum of whose elements is divisible by five”. A warm-up question would be to think about how many total subsets there are overall. The answer is 2 to the power 2,000. Even if we gave the brute-forcing approach all the time in the universe, it wouldn’t even come close to solving the puzzle. It is obvious that we need to be much more clever than simply guessing the answer. A rough approximation would be that a fifth of all total subsets would have a sum divisible by five. This is likely true, but the real challenge is to get a precise answer. To get a better understanding of the problem, it is helpful to start with a simpler example, like the set of one two three four five. By listing out all the two to the five subsets, it is clear that there are three distinct subsets that add up to six and three distinct subsets that add up to 10. In total, there are eight subsets with a sum divisible by five, including the empty set. This is more than the approximation of 6.4, suggesting that the true answer is a little bit bigger than expected. To solve the problem, one may try to understand the structure of the subsets or play around with how the sums are distributed mod 5. Alternatively, linear algebra approaches could be used. Ultimately, the lesson is more about the journey than the destination. All those are well and good, but instead my goal here is to teach you about something called a generating function. It’s one of those tactics where after the fact you can think, “Okay, yeah I get that this works, but how on earth would you have thought of that?” Honestly, I don’t know. There’s a time in your life before you understand generating functions and a time after and I can’t think of anything that connects them other than a leap of faith.
I’m going to ask you to consider the polynomial
$$1 + x \times 1 + x^2 \times 1 + x^3 \times 1 + x^4 \times 1 + x^5$$
Now I know you could rightfully ask where does this come from? What do polynomials have to do with things? What is the variable $x$ even supposed to represent right now? And essentially $x$ is purely a symbol, the only reason that we’ve written a polynomial here is that the act of algebraically expanding it is going to completely mirror the act of constructing subsets and importantly this grouping that we want, where subsets with the same sum are all bunched together kind of happens automatically when you do this and let me show you what I mean.
When you expand out this expression basically comes down to making five binary choices: which term from each parenthetical do you choose? If you choose the one from each of those parentheticals, that will correspond to the empty set where we don’t choose any of the elements. Whereas, if I choose the $x^1$ term and then ones from everything else, that will correspond to the singleton set that just contains the number one. Similarly, if I choose the $x^2$ term, but ones from everything else, that corresponds to the set just containing two. Just choosing the $x^3$ term corresponds to the set just containing the number three.
But, interestingly, notice what happens if I choose the $x^1$ term and the $x^2$ term and then ones from everything else. This corresponds to the choice of the subset that has one and two and nothing from everything else, but in the polynomial, the way it expands looks like $x^3$. So we have two different $x^3$ terms each of which came from a subset whose sum was three.
And, honestly, the pattern that I’m going for here is one that’s probably easiest if you just take the time to pause and think through for yourself what happens when you expand everything here. Essentially every possible subset corresponds to one of the terms in this expansion and then the critical point is that the exponent in the term that you get from that expansion equals the sum of that corresponding subset. Kind of confusing when you say it out loud, but again if you just kind of think it through yourself I think you can see what I mean.
For example, when all of the dust settles and we collect all 32 terms here, three of those terms are $x^{10}$ and each of those came from a choice of elements whose sum was equal to ten. Now normally when we write a polynomial, we collect together all like terms so instead of having three copies of $x^{10}$ we would just see the coefficient 3 in front of $x^{10}$. So each of these coefficients is a way of encoding the number of subsets with a particular sum.
So this, like I said at the start, is an example of something called a generating function where the idea is if you have some question with an answer associated with each positive integer. So, in our case, how many subsets add up to a particular value? When you construct a polynomial whose coefficients correspond to the answers to that question, you can get a surprising amount of insight from your original question by mathematically manipulating and analyzing the properties of this polynomial. But, for more general problems, this trick can be really useful.
There are tons and tons of examples of generating functions, but one especially fun example is the study of Fibonacci numbers, which can be expressed as an equation in terms of a function. This equation can be manipulated and, with a little partial fraction decomposition and geometric series power expansion, can be written in an exact closed form expression for each individual Fibonacci number.
In our particular problem, if we extend from the simple example with just one two three four five to the big example with all the numbers up to two thousand, our corresponding generating function involves two thousand different binomial terms, i.e. one plus x, one plus x squared, etc. If we were to expand this, the coefficients tell us all the information we want. However, it would be insane to actually expand it, so we can just think of it in the back of our minds.
By evaluating the function at x equals 0, we know that the answer is 1, and the coefficient in front of the x to the 25th term is 142, corresponding to the fact that there are 142 distinct subsets that have a sum of 25. By evaluating the function at x equals one, we can deduce the sum of all of the coefficients. This trick can be really useful for more general problems. But, it’s important to remember that mathematics is about the process of abstraction and generalization and here we’re seeing how that process can take us from a seemingly mundane counting question to a much deeper understanding of the structure of numbers.
Remember, each coefficient counts how many subsets have a certain sum, so when you add them up we’re counting all of the subsets which we know to be $2^{2000}$. However, I can give you a genuinely new fact if I ask you to evaluate this function at negative 1 - take a moment to think about what that means.
If you plug in negative 1, again we start with the thing we know, the factored expression up top, and here all you need is to look at the first term when you plug in $x$. The first parenthetical goes to zero, so the whole expression has to be zero, but what does that tell you when we apply it to the expanded expression using all of the coefficients?
In the spirit of being as suggestive as possible of the strange turns that this solution takes, I want you to really visualize the various powers of negative one in this expression in terms of rotations. The first term, negative one to the zero, is just one which we’ll picture as a vector from zero to one. Then negative one to the first power is just negative one itself which I want you to be thinking about as a 180 degree rotation away from that last term. Then when we take negative one squared, that’s positive one, again a 180 degree rotation and in general each successive term here looks like another rotation by 180 degrees.
Algebraically, what this translates to is that we have an oscillating sum between the even coefficients and the odd coefficients, but keep the visual in the back of your mind. This expression is true for any generating function, but again for our special generating function we know that this value, this alternating sum, should equal zero. And a way you can interpret that is that it’s telling you there’s an equal balance between the even coefficients and the odd coefficients. And, remember, maybe in the context of our smaller example these coefficients are encoding for us facts about subsets, so if there’s an equal balance between all those even coefficients and the odd coefficients it’s telling you that half of all the subsets have an even sum and half of them have an odd sum. That’s probably what you would expect, but it’s not obvious at first how you would show that and with the generating function it just kind of pops right out.
And, again, to be suggestive of where we’re going, let me rewrite this a little bit by taking the last two things we evaluated, add up those two and then divide by one half. If you think about it, this is a way of filtering out all of the even coefficients and killing all of the odd coefficients. So it becomes an especially clean way to write the fact that the sum of all of the even coefficients, which again in the back of your mind means the total number of subsets with an even sum, will look like half of the total.
This is, needless to say, tantalizingly close to the actual question we want to answer; what we would like to do is find some clever thing that we can do to the function $f$ some well-chosen numbers to evaluate it on so that we get all the coefficients corresponding to multiples of five. Again, thinking back to what these coefficients encode for us, that will be answering our final question that will be counting the total number of subsets whose sum is divisible by five.
The trick to doing this is to generalize what we just did, where the successive powers of the input were rotating back and forth, but this time we don’t want them to rotate every other time we’d like them to somehow rotate with a period of five and to do that we extend into the complex plane. You see up there we can find a value so that as we take successive powers of it it will rotate by a fifth of a turn, giving us a process with a frequency of five.
And, if you step back, I know that it’s kind of absurd that I’m asking you to think about complex numbers, I mean we started with a counting question. But, it’s important to remember that mathematics is about the process of abstraction and generalization and here we’re seeing how that process can take us from a seemingly mundane counting question to a much deeper understanding of the structure of numbers. Similarly, when you square zeta to the one you get zeta to the two, when you square zeta to the two you get zeta to the four and when you square zeta to the three you get zeta to the six.But, of course, we’re only interested in the fifth roots of unity so we have to loop around, so zeta to the four squared is zeta to the eight which is the same as zeta to the third and zeta to the six squared is zeta to the twelve which is the same as zeta to the one.
Discrete math can sometimes seem wild, but the trick we’re about to apply has a heavy resemblance to many other instances of using complex numbers to better understand discrete questions of integers. Specifically, the complex number I’m interested in is labeled zeta and it sits a fifth of a turn around the unit circle. This means its angle is two pi fifths radians and its magnitude is one. We can also think of it as having a real part of the cosine of 72 degrees and an imaginary part of the sine of 72 degrees.
These numbers have a special name, they’re called the fifth roots of unity, essentially because they solve the equation z⁵ = 1. When we add up these five terms, we’re just adding up the roots of unity themselves. If f(x) = x, for example, when we add up the five terms, the overall sum will loop back to be zero.
A slightly less trivial example would be if f(x) = x². When we square zeta to the zero, it stays zeta to the zero, which is just a fancy way of saying the number one. Similarly, when we square zeta to the one, we get zeta to the two, when we square zeta to the two, we get zeta to the four and when we square zeta to the three, we get zeta to the six. We have to loop around, so zeta to the four squared is zeta to the eight which is the same as zeta to the third and zeta to the six squared is zeta to the twelve which is the same as zeta to the one. When you square $\zeta$, you get $\zeta^2$ itself, so you might imagine this dot up here moving over to the $\zeta^2$ dot when we do it. $\Theta^2$ moves to $\zeta^4$, so you might imagine this dot moving over to $\zeta^4$. $\Theta^3$ moves to $\zeta^6$, which because we loop around every five times, is the same thing as $\zeta^1$. So this dot will move up here. And finally $\zeta^4$ squares to give us $\theta^8$ which reduces to be the same as $\zeta^3$, which I might draw like this.
That might seem a little confusing to think about, especially with all the arrows I have drawn here, but it’s worth thinking through at least once in your life, because the idea here is that when we square this, I go to all of these different terms and I program them to double the angle that they have, the overall effect is to just shuffle those terms. We get the same numbers but written in a different order, so their sum is still going to be zero. Similarly, if you go through this exercise with $x^3$, which I encourage you to do, and you follow around where each one of these dots will end up, you’ll be able to see that when we cube these terms, when we take each one and we multiply the angle that it has by three again, we just shuffle them around - same terms listed in a different order. Unsurprisingly, the same thing happens if our function was $x^4$, but critically where things change is if we consider the function $x^5$. In that case, when you raise $\zeta$ to the fifth power, by definition it goes to one. Similarly, $\zeta^2$ raised to the fifth power goes to one. All of these go to one, they are the roots of unity. This is, after all, their whole purpose in life. So in this case, when we apply the function and add them all up, instead of going to zero and getting cancellation, we get a kind of constructive interference. All of them equal one so their sum is equal to five.
So if you step back and think about what all those examples mean, essentially this expression is something that will go to zero for powers of $x$ which are not divisible by five, but it goes to something non-zero for powers of $x$ which are divisible by 5 and that’s exactly the kind of filter that we’re looking for. If you’re worried that our actual function is much more complicated than a simple power of $x$, essentially things play really nicely here because everything is linear. If $f$ is some massive polynomial and we want to evaluate this big sum, you could sort of think of going column by column, where each time you really are just adding up powers of $\zeta$ and in most cases all those powers cancel out with each other and you get zero, but when all of those powers are multiples of five they constructively interfere and instead you get five times whatever the corresponding coefficient is.
Deep in the weeds it’s easy to forget why we’re here in the first place, but remember each one of those coefficients tells us how many subsets add up to a certain value and so what we want is to add up all of the coefficients that are multiples of five and what we have right now is a way to explicitly do that. If we evaluate this function on these five different routes of unity (which I know seems kind of weird), then all we have to do is divide by five and it gives us the sum that we want. That’s really cool if you ask me. We have a question that’s just about subsets, it’s a discrete math problem, and yet the way that we can answer it is to evaluate a crazy polynomial on some judiciously chosen complex numbers. The more math you do the less crazy that seems because complex numbers have this bizarre relationship with discrete math, but it really is wonderful - there’s no two ways about it. However, some of you might complain that the only way that this is useful is if we can actually evaluate this wild expression on our polynomial. Now, remember, the form of the polynomial we know the one we’re comfortable with is the factored form where you have this one plus x one plus x squared on and on all the way up to one plus x to the two thousand. Everything up to this point is just meaningless symbolic play pushing around one hard problem into another unless we can actually roll up our sleeves and do some honest calculation here. This is the final thrust in our argument so step back, take a deep breath. It’s actually not as bad as you might think, but let’s start just by thinking about how you might evaluate just one of the roots of unity that we need, maybe zeta itself.
So what that looks like is one plus zeta times one plus zeta squared times one plus a to cubed on and on except, importantly, after those first five terms everything starts repeating, because powers of zeta repeat the entire expression up to 2000 is basically just going to be a copy of this expression 400 times. It still might seem hard to evaluate this expression, but it’s way easier than multiplying out 2,000 different terms. A way you might visualize this is that we’re taking each one of those roots of unity but basically adding one, we’re shifting them all to the right. This picture actually lends itself to a really nice geometric intuition for the numerical answer that we might expect. The thing that we want is the product of these five different complex numbers, these five yellow dots and if you know a thing or two about complex numbers since these come in conjugate pairs all we really need is to multiply the lengths of these five yellow lines.
For example, that dot furthest to the right corresponds to one plus zeta to the fifth, which in the diagram I’m labeling as zeta to the zero plus one, but it doesn’t matter in either case they’re both just fancy ways of writing the number two. Next to that, we have the values one plus zeta and one plus zeta to the fourth, both of which have the same magnitude. The lengths of these lines are the same and let’s just give that a name L1. So we need to multiply two different copies of that length L1 squared. Similarly, the remaining two values theta squared plus one and zeta cubed plus one, they also have the same length and they’re a conjugate pair so let’s just call that length L2. So our product needs to include two copies of that L2.
If we were just making a loose heuristic guess you might notice that L1 is a length that’s something a little bit longer than one and L2 is something a little bit shorter than one, so the final answer here probably comes to something around two ish. We’re not positive, but something in that ballpark. To turn this into an exact answer we could just expand out the full expression. It’s honestly not that bad there’s only 32 different terms.
Okay, you’ve hung with me for a long time now, and I know that it’s getting to be a lot. But there’s one final trick in this whole argument that makes our last step much simpler than you might think it should be. And let’s just recap to remind ourselves of where we are. We started with this question asking us to count the number of subsets of 1 up to 2 000 whose sum is divisible by five. We then constructed this polynomial whose coefficients tell us how many subsets have a particular sum for each value n. So what we want is to add up every fifth coefficient of that polynomial. Then we saw how evaluating this polynomial as a function on all of the fifth roots of unity, then adding them up, ends up giving us exactly this filter that we want. And here we’re evaluating just one of those terms, f(zeta), which essentially comes down to a product of five complex numbers.
As a super slick way to actually evaluate that product, here’s the final trick. Remember, I described these numbers as roots of unity, they solve the equation $z^5 = 1$. Another way to think about that is that they are roots of the polynomial $z^5 - 1$. This means that we can factor the polynomial $z^5 - 1$ to look like this, where there’s one factor corresponding to each one of the roots; you take $z -$ each one of the roots. This expression is magical when you think about all of the crazy cancellations that has to happen when you expand it all out, but it is true and it’s useful for us right now. Because the expression on the right-hand side looks almost identical to the thing we need to evaluate. The trick is to plug in $z = -1$. If you do that, you have the negative of what we want, so if you multiply it by -1, the left-hand side becomes 2. And then the right-hand side turns into the thing that we want to evaluate. So, just as our geometric intuition earlier might have suggested, not only is the answer around two, the answer quite magically turns out to be precisely two.
This is super nice and very lovely, because it means this bigger expression that we want to evaluate, where we’re adding up $f$ on all of the different roots of unity, we know its value on the first root of unity. It will be $2^{400}$. Essentially identical reasoning shows that its value on the next three roots of unity is also $2^{400}$. The only one that’s different is when we evaluate it at $\zeta^0$, which is a fancy way of saying the number one, and we know how to evaluate this at one. All of these parentheticals turn into two, so it looks like taking two multiplied by itself two thousand times.
And so finally with that, we have a highly explicit honest answer to our counting question. To add up all of these coefficients which are divisible by five, which remember is a way of counting how many total subsets have a sum divisible by five, the answer is one-fifth of this weird complex expression, which we just computed to be $2^{2000}$ plus four different copies of $2^{400}$.
Here, you might want to do just a quick sanity check on does this answer make any sense. For example, if you do it in the smaller case with the set {1, 2, 3, 4, 5} and you walk through all the same reasoning that we just did, it tells you that the answer is one-fifth of $2^5$, the total number of subsets, plus four times two to the one, in this case, which is a fifth of 32 plus 8, which is 8. And if you’ll remember when we explicitly looked at them all that was in fact the answer.
Look, this is a hard puzzle, and when it’s worth putting in the time to solve a hard problem it’s also worth taking some time to reflect on it. What do you get out of this? What’s the takeaway? You could reflect on the answer itself, how the dominant part is indeed one-fifth of all the total subsets like we might have guessed, and how this error term came about from the not-quite-destructive interference in a massive combination of roots of unity. But again, what makes this question interesting is not the answer, it’s the way that we solved it. Namely, taking a discrete sequence that we want to understand and treating it as the coefficients on a polynomial, then evaluating that polynomial on complex values. Both of those steps are probably highly unexpected at the outset. Both of the steps we discussed relate to powerful and general techniques found elsewhere in mathematics, such as the way primes are studied leading up to the Riemann hypothesis. This is a complex topic, and it would be a shame to rush through it, so let’s take the time to make the video I promised about the zeta function.
The two ideas are parallel: just like our subsets puzzle, the way Riemann studied primes involved a discrete sequence that carries information about prime numbers, and then considering a function whose coefficients are the terms in that sequence. This function is known as a Dirichlet series, and by studying how it behaves with complex-valued inputs, we can suss out information about the coefficients.
Complex numbers are useful in this way because they offer more power in making deductions about the coefficients, and in particular, the use of values on the unit circle (or roots of unity) to detect frequency information is extremely fruitful. This core idea underlies Fourier transforms, Fourier series, and the topics that follow from those.
If you want to learn more, I highly recommend the book Generatingfunctionology by Herbert Wilf. I’ll also leave up a few puzzles on the screen for anyone who wants to practice with the idea.