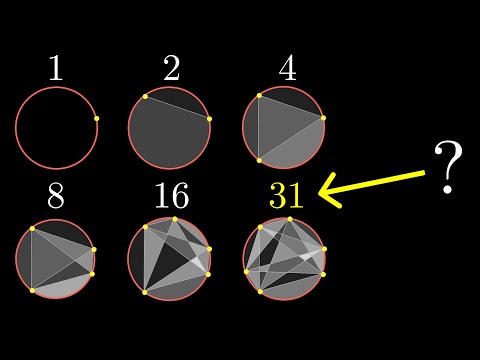
Moser’s Circle Problem is a very famous cautionary tale in math. Some of you may have seen it before, but what I want to do here is to explain what’s going on.
We start by taking a circle and putting two points on it, connecting them with a line that is a chord of the circle. This divides the circle into two different regions. If we add a third point and then connect it to the previous two points with two more chords, the lines divide the circle into four separate regions. If we add a fourth point and connect it to the previous three, we end up with eight regions. Adding a fifth point to the circle, connecting it to the previous four, results in a total of 16 regions. have thought about it’s a little bit of a tricky twist and you can use it to solve the problem
You can naturally guess what might come next, but would you bet your life on it? At a sixth point, if you connect it to all the previous ones and carefully count up all the different regions, you end up not with the power of two you might have expected, but just one shy of it.
Some of you might be raising your hand saying, “Doesn’t it depend on where we put the points?” For example, watch how this middle region disappears if we place everything nice and symmetrically around the circle. So, yes it does depend, but we’re going to consider the cases where you never have any three lines intersecting with each other. This would be the generic case if you just choose n random points; almost certainly, you’ll never have three lines coincide.
Setting aside the technical nuances, the problem is such a tease: it looks so convincingly like powers of two until it just barely breaks. I have such a strange soft spot for this particular question; when I was younger, I wrote a poem and a song about it.
On the one hand, it’s kind of silly because this is just one example of what the mathematician Richard Guy called the Strong Law of Small Numbers, summed up in the phrase, “There aren’t enough small numbers to meet the many demands made of them”.
I think what I really like about this problem is that if you sit down to try to work out what is the real pattern, what’s actually going on here, it’s just a really good exercise in problem solving, so it makes for a nice lesson right here. But also, it’s not just a coincidence that it starts off being powers of two - there’s a very good reason this happens, and it’s also not a coincidence that you seemingly randomly hit another Power of Two a little bit later on the 10th iteration.
So, we’ve got this pattern and what you want to find is what function describes it. If you put n points on the boundary of a circle and you connect them with all the possible chords and you count how many regions the circle has been cut into, if the answer isn’t a power of two, what is it? What function of n should we plug in?
As always with math problem solving, rule number one if you’re stuck is to try solving easier questions somehow related to the problem at hand. It helps you get a foothold, and sometimes those answers are helpful in the final question. In this case, two warm-up questions that come to mind are: how many total chords are there in this diagram and at how many points within the circle do those chords intersect each other?
The first question is relatively friendly: every one of those chords corresponds uniquely with a pair of points on the circle, so effectively what you want to do is count how many distinct pairs of points are there. There is a function that does this; it’s called n choose two. By definition, this counts the number of distinct pairs that you can choose from a set of n items, where order doesn’t matter. To calculate it, the way you often think about it is that you have n choices for what your first item should be, and then you have n minus 1 options for what that second item should be. But simply multiplying those would over count, since for a given pair, you would have two distinct ways to arrive at that pair, and remember we don’t care about order. To account for this, you divide by two.
For example, 7 choose 2 would look like 7 times 6 divided by 2, which is 7 times 3 or 21, and if you count up the number of distinct pairs of seven items, there are indeed 21 of them.
Counting the number of intersection points in the diagram is a little bit trickier. One idea might be that it should be the number of pairs of chords, since every intersection point comes from two different chords. However, that would not quite be right, because the association is not unique; you can find a pair of chords that don’t intersect within the circle. As I said, it’s a little bit tricky - I’d encourage you to try to pause and think about it for yourself.
And if you do that, you give yourself a moment - maybe if you’re a little bit lucky - here’s one thing you might not have thought about: it’s a little bit of a tricky twist, and you can use it to solve the problem. If you’ve never seen this before and you want to know why it’s true, there’s a really lovely argument I’ll leave it up as an exercise. But, moving on to the second thing we need to know, notice what happens when you add up the rows of this triangle: you get 1, then 1 + 1 = 2, 1 + 2 + 1 = 4, 1 + 3 + 3 + 1 = 8, and as you continue on you always get powers of two.
At this point, you might be a little gun shy about jumping to conclusions about powers of two too quickly, but in this case it’s a genuine pattern - there’s no trickery being pulled. There are a few ways that you can think about why there should be powers of two here, but one that I like is to think about how as you go from that first row to the next one, it’s like the number one is sort of donating two copies of itself into the next row. Likewise, as you go from the second row to the third, each of those ones is donating two copies of itself to the next row. In general, as you go from one row to the next, each number donates two copies of itself to the one below.
So, as you add up the totals for each of these rows, it stands to reason that those totals double on each iteration. Circling back to our original question, think about what this means. The answer to our question looked like 1 + n choose 2 + n choose 4. In the context of Pascal’s triangle, you could think about that as adding up the zeroth, second, and fourth terms inside some row of that triangle. For instance, when n is equal to 5, it looks like adding up 1 + 10 + 5.
Now, because each of those numbers is the sum of the two above it, this is the same thing as adding up the first five elements in the previous row, which in this case is adding up the entire previous row. Hence why it’s a power of two. Same deal for all the numbers that are five or less.
When you situate this formula inside Pascal’s triangle and you relate it to the previous row, what you’re doing is adding up the entirety of that previous row. The point at which this breaks is for n equals 6, because in that case when you relate this to the previous row, adding up the first five elements of that row doesn’t cover the whole thing - it falls short specifically by just one.
And notice what happens when we plug in n equals 10. Looking down at the tenth row and relating those terms to the previous one, adding the first five elements of the ninth row is exactly half of that row. Because the triangle is symmetric, this means that when you add them up you get exactly half of a power of two, which itself of course is another power of two.
As a challenge problem for you, I don’t actually know if this is the last time that you’ll ever see a power of two. Maybe one of you out there who’s clever with diophantine equations than I am can come up with some clever proof.
Stepping back to summarize, we started by counting the total number of chords and the total number of intersection points, which by thinking about the right associations is the same as computing n choose 2 and n choose 4. # Euler’s Formula and the Moser’s Circle Problem
Bringing in Euler’s formula, we can get an exact closed form expression for the number of regions inside the circle. Connecting that with Pascal’s triangle gives us a more intuitive understanding of why powers of two break when they do. So, Moser’s Circle problem is a cautionary tale about being wary of patterns without proof, but at a deeper level it also tells us that what is sometimes chalked up to be coincidence still leaves room for satisfying understandings.
By the way, the Summer of Math Exposition is indeed happening again this year! If you have any interest in making an online math explainer of some form - whether that’s a video, an article, or anything else you dream up - the last two years have proven that this is a great way to get more eyes on your work. Additionally, there are opportunities for cash prizes thanks to the generosity of this year’s sponsor, Jane Street. You can find all the information you need at sum.3b1b.co and I’ll also leave other relevant links in the description, so do check them out. It was a ton of fun the last two years and I’m very excited to see what people come up with this year!